개요
오랜만에 포스팅을 작성합니다.
그동안 프로젝트의 방향성에도 변동이 잦았고, 필요 기능을 구현하기 위한 기술을 선택하는 과정에서 많은 시행착오를 겪었습니다.
이번 포스팅에는, 기타 사운드 분류 로직을 구현하면서 겪은 시행착오와, 최종적으로 채택한 YAMNet 모델과 TFLite를 활용한 방법을 공유하고자 합니다.
기타 사운드 분류 로직이 뭔가요?
저는 의도적으로 제가 만들고 있는 통칭 기타 연주 앱 프로젝트가 정확히 무엇인지 말씀드리지 않고 있습니다.
실제 출시가 목적이기도 하고, 대상 타겟이나 필요 기능 우선순위가 꾸준히 바뀌어 명확히 말씀드리기 어려운 것도 사실입니다.
하지만, 프로젝트 구상 초기부터 필수로 개발해야 하는 기능이 있었는데, 그중 하나가 바로 입력되는 오디오 데이터가 기타 사운드인지, 아니면 이외의 소음인지 구분하는 필터링 기능입니다.
사실, 이 기능을 간단하게 해결하는 방법이 있긴 합니다.

애초에 기능을 구현할 필요가 없는 환경을 대상으로 앱을 개발하면 됩니다.
오디오 인터페이스를 사용하면, 케이블로 연결된 순수한 기타 사운드를 컴퓨터로 입력받을수 있어, 마이크 캡쳐 처럼 소음의 걱정이 아예 없습니다.
하지만, 제 앱의 타겟은 오디오 인터페이스 사용자들이 아니며, 최대한 다양한 타겟을 흡수하기 위해 마이크 캡쳐를 사용하는 것이 좋다고 판단했습니다. 애초에 모바일 앱이라 오디오 인터페이스를 사용할 수 없는 환경인 것도 있습니다. (가능하긴 하나 어려움)
.. 그렇게 삽질이 시작되었습니다.
V1. 룰 베이스 기반 로직
첫번째 시도로, AI를 활용하지 않고, 룰-베이스 기반으로 기타 사운드 분류 로직을 개발했었습니다.
이 분류 로직은, 이전 포스트에서 소개한 오디오 데이터 스트림을 적극 활용하여, 소리의 구성 성분을 파악해 이 소리가 기타 소리인지, 아니면 그 외의 소리인지 구분하는 방식입니다.
후술할 실제 구현은 복잡하지만, 핵심 아이디어는 간단했습니다.
- 진폭(볼륨)이 너무 낮거나 높진 않은가?
- 주파수의 높낮이가 기타 가역 범위 내에 있는가? (일반적 형태의 6현 기타의 경우, 통상적으로 80Hz~1300Hz 사이)
- FFT 스펙트럼에서 기타만의 특징(배음 구조)이 보이는가?
이 세 가지 조건을 모두 만족하면 기타 소리로 판단하고, 그렇지 않으면 그 외의 소리로 판단하는 방식입니다.
실제로 이 조건 중 앞의 1, 2번 조건은 과거 AudioKit 라이브러리를 소개하는 포스트에서 이미 구현된 거나 다름 없었습니다.
단순히 특정 필터를 거치기만 하면되기 때문입니다.
하지만, FFT 스펙트럼에서 기타만의 특징을 찾는 것은 상당히 어려웠습니다.
배음이란?
배음(Overtone)은 물체가 진동할 때 발생하는 기본적인 음인 기음(Fundamental Tone)의 정수배 주파수를 가진 음들을 말합니다. 모든 소리는 단 하나의 주파수로 이루어진 것이 아니라, 기음과 함께 여러 개의 배음이 복합적으로 섞여 있습니다.
이 배음들이 어떻게 구성되고 얼마나 강한지에 따라 소리의 질감, 즉 음색(Timbre)이 결정됩니다.
특히, 기타나 바이올린과 같은 현악기는 줄의 양 끝이 고정되어 있어 진동이 반사되며 특유의 파동을 형성합니다. 이때 줄 전체가 한 번에 진동하는 것이 기음이며, 동시에 1/2, 1/3, 1/4 등 여러 부분으로 나뉘어 진동하는 것이 배음입니다.
FFT 스펙트럼으로 배음 파악하기
배음은 소리의 질감, 즉 음색(Timbre)을 결정하는 중요한 요소이지만, 추상적인 개념입니다.
이 추상적인 배음 구조를 시각적으로 확인하기 위해 FFT(고속 푸리에 변환)가 필요합니다.
FFT는 시간 영역의 복합적인 소리 신호를 주파수 영역으로 변환하여, 소리를 구성하는 기음과 모든 배음의 주파수 및 상대적인 크기(진폭)를 정량적으로 분석해 줍니다.
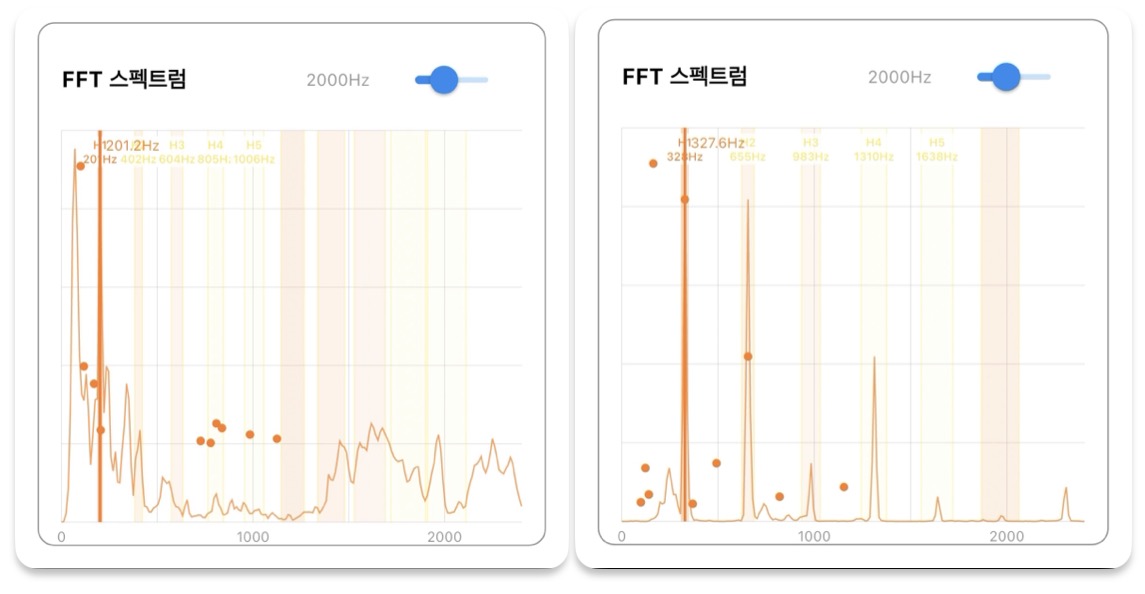
위 두 스크린샷은 제가 만든 테스트 앱에서 기타 사운드와 생활 소음의 FFT 스펙트럼 변화를 비교한 것입니다.
(왼쪽) 생활 소음은 불규칙한 봉우리들이 마치 산맥과도 같은 형태를 띄지만, (오른쪽) 기타를 연주할 때는 규칙적인 간격으로 높게 솟은 봉우리들이 나타납니다.
이 규칙적인 봉우리들이 바로 현악기 특유의 배음 구조가 시각적으로 표현된 모습이며, FFT 스펙트럼을 통해 기타 소리를 분류할 수 있다는 아이디어가 여기서 시작되었습니다.
실제 구현
이제 본격적인 룰 베이스 버전의 기타 사운드 분류기의 구현을 소개드립니다.
앱 전체에서의 파이프라인
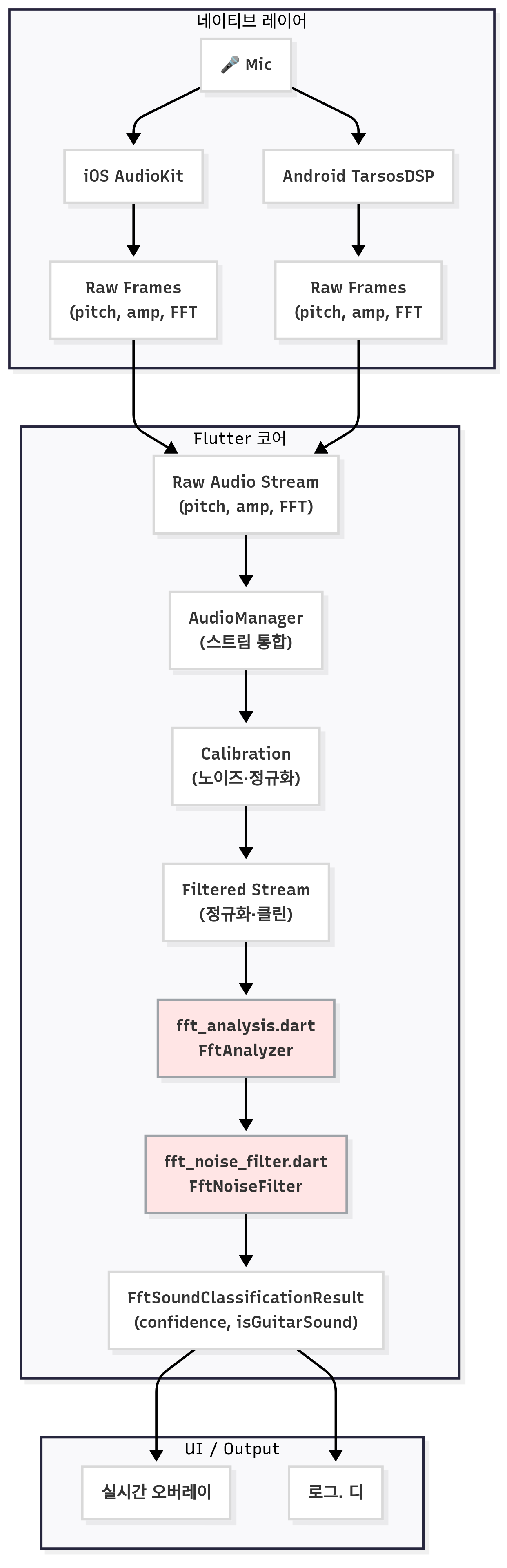
위 다이어그램은 앱 전체에서의 파이프라인에서 기타 사운드 분류 로직이 위치한 부분을 나타낸 것입니다.
붉은색으로 하이라이트 처리된 fft_analysis.dart 와 fft_noise_filter.dart가 이번 포스팅의 주인공으로,
이전 포스트에서 소개드린 중앙화된 오디오 스트림으로부터 이어집니다.
각 네이티브 라이브러리 영역 -> 플러터 코어로 이어진 중앙화 스트림에서, 정규화된 세가지 오디오 데이터(FFT, Pitch, 진폭)를 받아, 로직이 입력된 데이터가 기타 사운드인지, 아닌지 판별합니다.
분류기 로직의 내부 파이프라인
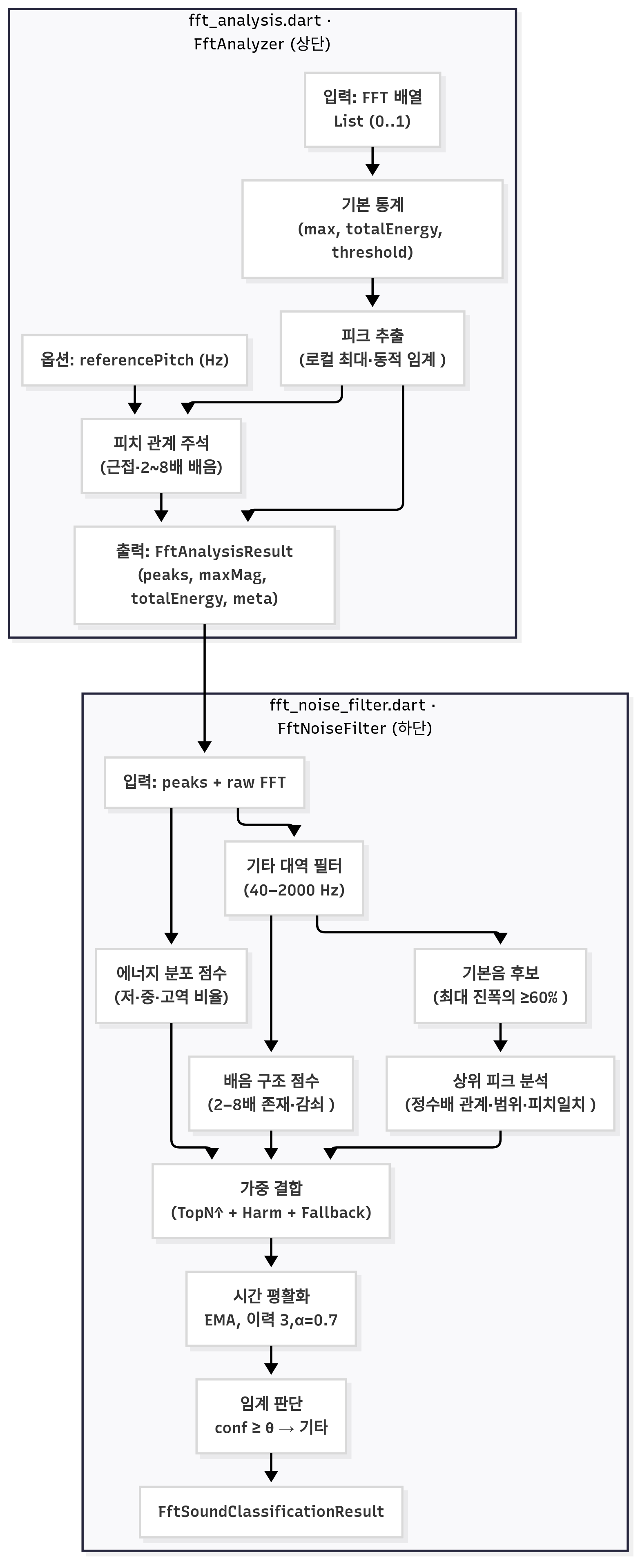
위 다이어그램은 전체 구조도에서 표현한 fft_analysis.dart 와 fft_noise_filter.dart 의 내부 파이프라인을 나타낸 것입니다.
실제 소스 코드와 함께, 다이어그램 내부의 각 파이프라인이 어떻게 흘러가는지 설명드립니다.
입력과 결과
//fft_noise_filter.dart
FftSoundClassificationResult analyze(
List<double> fftData, {
double? currentPitch,
DateTime? timestamp,
}) { ... }
내부 로직은 복잡할지 모르지만, 결국 이 기타 사운드 분류기도 오디오 스트림에 설치되는 함수 형태에 불과합니다.
입력 값은 정규화된 FFT 스펙트럼 데이터를 필수로 받고, 로깅 용 타임스탬프, 그리고 현재 피치 정보(삼중 오디오 스트림 데이터에서 추출한 값)를 선택적으로 받습니다.
피치 값은 입력된 경우 후술할 FFT 스펙트럼 분석 로직에서 참고용 데이터로 활용될수 있습니다.
//fft_noise_filter.dart
class FftSoundClassificationResult {
/// 0.0~1.0 신뢰도. 후단에서 임계값과 비교해 isGuitarSound를 결정합니다.
final double confidence;
/// 최종 이진 판정(임계값 이상이면 true)
final bool isGuitarSound;
/// 분석 시각(로그·동기화 용도)
final DateTime timestamp;
/// 부가 메타(피크/배음/분포/최대진폭 등 디버깅에 유용)
final Map<String, dynamic>? metadata;
const FftSoundClassificationResult({
required this.confidence,
required this.isGuitarSound,
required this.timestamp,
this.metadata,
});
}
결과 클래스는 더 간단합니다.
confidence 값은 0.0~1.0 사이의 신뢰도를 나타내며, 이 값이 임계값 이상이면 isGuitarSound 값이 true가 됩니다.
설정 초기화
//fft_noise_filter.dart
void init({
double guitarConfidenceThreshold = 0.45,
double minGuitarFreq = 40.0,
double maxGuitarFreq = 2000.0,
int minRequiredHarmonics = 2,
int maxHistorySize = 3,
double temporalSmoothingFactor = 0.7,
}) { ... }
confidence 값에 대한 기준점, 그리고 최소/최대 피치 주파수 필터 범위(6현 기타의 통상 가역대역인 40~2000Hz), 그리고 필수 배음 개수와 최대 이벤트 기록 개수 및 스무딩 파라미터를 설정할 수 있습니다.
여기까지는 설정 및 입출력에 대한 설명이었습니다. 이제 실제 로직이 어떤 흐름으로 진행되는지 알아봅시다.
FFT 스펙트럼 전처리
//fft_analysis.dart
FftAnalysisResult analyzeSpectrum(FftAnalysisInput input) {
if (input.fftData.isEmpty) return _createEmptyResult();
// 1) 기본 통계(최대 진폭, 전체 에너지, 동적 임계값 계산)
final stats = _calculateBasicStats(input.fftData);
// 2) 중요한 피크 추출(기타 대역 내 로컬 최대 & 임계 이상)
final peaks = _extractSignificantPeaks(input.fftData, input.referencePitch);
// 3) 결과 구성(피크 + 통계 + 메타)
return FftAnalysisResult(
peaks: peaks,
maxMagnitude: stats['maxMagnitude'] as double,
totalEnergy: stats['totalEnergy'] as double,
minFreq: _minGuitarFreq, maxFreq: _maxGuitarFreq,
metadata: {
'analysisTime': input.timestamp,
'sampleRate': _sampleRate, 'fftSize': _fftSize,
'peakThreshold': stats['dynamicThreshold'],
'referencePitch': input.referencePitch,
},
);
}
위 구조도를 보셔도 알겠지만, 기타/비기타 소리를 분석하는 메인 분석기인 fft_noise_filter.dart에 도달하기 전에 fft_analysis.dart가 해주는 역할들이 있습니다.
fft_analysis.dart는 입력된 FFT 스펙트럼 데이터를 기반으로, 기타/비기타 소리를 분석하기 전에 우선 FFT 스펙트럼이 어떤 형태로 이루어져있고, 특징점이 있는지 파악하는 책임을 수행합니다.
fft_nosie_filter.dart가 제대로 된 요리를 만들기 전, 원래료를 깎고 손질하는 역할을 fft_analysis.dart가 담당한다고 보시면 됩니다.
위 함수는 fft_analysis.dart의 최상위 함수입니다. 빈 결과를 생성하고, 두가지 전처리 함수 (_calculateBasicStats, _extractSignificantPeaks)를 호출하여 최종 결과를 도출하는 역할을 맡습니다.
//fft_analysis.dart
/// FFT 데이터의 기본 통계 계산
Map<String, dynamic> _calculateBasicStats(List<double> fftData) {
double maxMagnitude = 0.0;
double totalEnergy = 0.0;
int validBinCount = 0;
// 기타 주파수 범위에 해당하는 빈만 계산
final double binWidth = _sampleRate / (_fftSize * 2);
final int minBin = (_minGuitarFreq / binWidth).floor();
final int maxBin = math.min((_maxGuitarFreq / binWidth).ceil(), fftData.length - 1);
for (int i = minBin; i <= maxBin; i++) {
final magnitude = fftData[i];
// NaN 값 처리
if (magnitude.isNaN || magnitude.isInfinite) continue;
totalEnergy += magnitude;
validBinCount++;
if (magnitude > maxMagnitude) {
maxMagnitude = magnitude;
}
}
// 동적 임계값 계산
final dynamicThreshold = math.max(
maxMagnitude * _thresholdRatio,
_absoluteMinThreshold,
);
// 실제 사용할 임계값
final finalThreshold = math.max(dynamicThreshold, _magnitudeThreshold);
return {
'maxMagnitude': maxMagnitude,
'totalEnergy': totalEnergy,
'averageEnergy': validBinCount > 0 ? totalEnergy / validBinCount : 0.0,
'validBinCount': validBinCount,
'dynamicThreshold': finalThreshold,
};
}
_calculateBasicStats 함수는 입력된 FFT 스펙트럼 데이터를 기반으로, 최대 진폭, 전체 에너지, 동적 임계값을 계산합니다.
쉽게 말씀드리자면, 포스팅 초반에 보여드린 FFT 스펙트럼의 시각적 형태로 예시를 들면, “이 프레임의 스펙트럼이 얼마나 세고, 또 어디까지가 의미 있는 봉우리인가”를 한번에 잡아주는 준비 단계라고 할수 있습니다.
사전에 설정한 기타 유효 대역(기본 설정은 40~2000Hz)에 해당하는 빈 내에서, 가장 큰 진폭은 어떤 구간인지, 전체 에너지의 양은 어떠한지, 유효 빈의 개수는 몇인지 파악한 후, 동적 임계값을 계산합니다.
이 과정이 필요한 이유는, 입력 레벨(마이크에 수신되는 녹음 크기)이 바뀌어도, “의미 있는 봉우리”만 뽑기 위한 기준선을 만들어야 하기 때문입니다.
//fft_analysis.dart
List<FftPeak> _extractSignificantPeaks(List<double> fftData, double? referencePitch) {
final double binWidth = _sampleRate / (_fftSize * 2);
// 기타 대역 내 빈 범위만 검토
final int minBin = math.max(1, (_minGuitarFreq / binWidth).floor());
final int maxBin = math.min(fftData.length - 2, (_maxGuitarFreq / binWidth).ceil());
final stats = _calculateBasicStats(fftData);
final threshold = stats['dynamicThreshold'] as double;
final List<FftPeak> candidates = [];
for (int i = minBin; i <= maxBin; i++) {
final mag = fftData[i];
// 동적 임계 이상 & 양옆보다 큰 로컬 최대(봉우리)
if (mag >= threshold && mag > fftData[i - 1] && mag > fftData[i + 1]) {
final freq = i * binWidth;
if (freq >= _minGuitarFreq && freq <= _maxGuitarFreq) {
candidates.add(FftPeak(frequency: freq, magnitude: mag, binIndex: i, metadata: {'isLocalPeak': true, 'binWidth': binWidth}));
}
}
}
// 진폭 내림차순 정렬 후 TOP-N 제한으로 비용 제어
candidates.sort((a, b) => b.magnitude.compareTo(a.magnitude));
final finalPeaks = candidates.take(_maxPeaks).toList();
// (옵션) 기준 피치와의 관계 주석(근접/배음 추정)
if (referencePitch != null && referencePitch > 0) {
_addReferencePitchInfo(finalPeaks, referencePitch);
}
return finalPeaks;
}
의미있는 기준선을 정했다면, 이제 그중에서도 뚜렷한 봉우리를 찾아내는 작업이 필요합니다.
이 함수는 직전에 계산한 “동적 임계값(threshold)” 이상이면서 “양옆보다 큰 로컬 최대”인 지점만 후보에 넣습니다.
이 후보들을 진폭 내림차순으로 정렬하고, 최대 피크 개수를 제한하여 비용을 제어하며, refrencePitch(참고용 피치 데이터)가 존재하면 각 피크에 “기준 피치 근접/배음(2~8)배” 여부를 주석으로 달아줍니다.
FFT 스펙트럼의 모든 피크가 아닌 로컬 최대 피크만 추출하는 이유는, 한 칸만 주변보다 높아도 피크처럼 보이는 값(미세 잡음)을 걸러내고, 실제로 높은 봉우리만 걸러내기 위함입니다.
요약하자면, 산맥(스펙트럼) 내에서 사전이 지정한 선(동적 임계값) 보다 높고, 동시에 양옆보다 뚜렷하게 높은 봉우리들을 골라 Top-N 순위를 매기는 작업입니다.
저는 이 과정을 유의미한 피크 추출이라고 부르고 있습니다.
기타/비기타 사운드 분류
이제까지는 FFT 스펙트럼(및 피치 데이터)를 통해 분석을 위한 원재료 가공 단계였습니다.
동적 임계치와 주요 피크가 추출되었다면, 이제 이 데이터로 기타/비기타 사운드를 분류하는 작업을 진행합니다.
메인 파이프라인
//fft_noise_filter.dart
FftSoundClassificationResult analyze(
List<double> fftData, {
double? currentPitch, // (옵션) 현재 피치: 일치/옥타브 매칭 가점
DateTime? timestamp, // (옵션) 분석 시각
Map<String, dynamic>? attackInfo, // (옵션) 어택 메타(로깅용)
}) {
_ensureInitialized();
if (!_isActive || fftData.isEmpty) {
// 비활성/빈 입력은 즉시 비기타로 반환(안전가드)
return FftSoundClassificationResult(confidence: 0.0, isGuitarSound: false, timestamp: timestamp ?? DateTime.now());
}
// 1) 피크 추출(fft_analysis.dart) — 전처리·동적 임계·로컬 최대 탐지
final fftAnalysisResult = _fftAnalyzer.analyzeSpectrum(FftAnalysisInput(
fftData: fftData, referencePitch: currentPitch, timestamp: timestamp,
));
final List<FftPeak> peaks = fftAnalysisResult.peaks;
// 2) 기타 유효 대역만 남기기(대역 필터)
final guitarRangePeaks = peaks.where((p) => p.frequency >= _minGuitarFreq && p.frequency <= _maxGuitarFreq).toList();
// 3) 기본음 후보(최대진폭의 60% 이상 피크)
final fundamentalCandidates = _identifyFundamentalCandidates(guitarRangePeaks);
// 4) 상위 피크 기반 점수(정수배 관계·범위·피치 일치)
final topPeaksScore = _analyzeTopPeaks(guitarRangePeaks, fundamentalCandidates, currentPitch)['score'] as double;
// 5) 에너지 분포 점수(저·중·고역 비율, Fallback용)
final energyDistributionScore = _analyzeFrequencyDistribution(fftData);
// 6) 배음 구조 점수(2~8배 존재·감쇠 패턴)
final harmonicStructureResult = _evaluateHarmonicStructure(guitarRangePeaks, fundamentalCandidates);
final harmonicScore = harmonicStructureResult['harmonicScore'] as double;
final harmonicCount = harmonicStructureResult['harmonicCount'] as int;
// 7) 가중 결합(TopPeaks 중심) + 필요 시 Fallback 채택
double finalConfidence = 0.0;
Map<String, dynamic> metadata = {};
bool usedFallbackLogic = false;
if (fundamentalCandidates.isNotEmpty) {
// 기본: TopPeaks 0.7 + Harmonic 0.3
final bestFundamental = fundamentalCandidates.reduce((a, b) => a.magnitude > b.magnitude ? a : b);
finalConfidence = topPeaksScore * 0.7 + harmonicScore * 0.3;
// 배음 수 부족/TopPeaks 약할 때 분포 기반 대체 점수 고려
if (harmonicCount < _minRequiredHarmonics || topPeaksScore < 0.3) {
final fallbackScore = (harmonicScore * 0.4) + (energyDistributionScore * 0.5) + (bestFundamental.magnitude * 0.1);
if (fallbackScore > finalConfidence) {
finalConfidence = fallbackScore;
usedFallbackLogic = true;
}
}
metadata['fundamentalFrequency'] = bestFundamental.frequency;
metadata['usedFallbackLogic'] = usedFallbackLogic;
} else {
// 기본음 후보 자체가 없으면 분포 점수 위주로 보수적 판정
finalConfidence = math.max(topPeaksScore * 0.5, energyDistributionScore * 0.4);
metadata['fundamentalFrequency'] = null;
metadata['usedFallbackLogic'] = true;
}
// 8) 시간 평활화(EMA) — 순간 노이즈/미스를 흡수해 안정화
final smoothedConfidence = _applyTemporalSmoothing(finalConfidence);
// 9) 임계값 비교 → 최종 판정
final result = FftSoundClassificationResult(
confidence: smoothedConfidence,
isGuitarSound: smoothedConfidence >= _guitarConfidenceThreshold,
timestamp: timestamp ?? DateTime.now(),
metadata: metadata,
);
_addToHistory(result); // 이력 유지(EMA용)
return result;
}
위 함수가 바로 기타/비기타 사운드 분류를 위한 메인 파이프라인입니다.
함수 내부에는 결과를 도출하기까지의 과정이 여러 단계로 이루어져 있습니다.
- FFT 스펙트럼 전처리(fft_analysis.dart. 직전까지 설명했던 과정)
- 기타 유효 대역만 남기기(대역 필터)
- 기본음 후보 식별(fundamentalCandidate)
- 상위 피크 기반 점수(topPeaksScore)
- 에너지 분포 점수(energyDistributionScore)
- 배음 구조 점수(harmonicScore)
- 가중치 결합.
- 시간 평활화. 안정화 단계.
- 임계값 비교 및 최종 결과 도출.
기본음 후보 식별
//fft_noise_filter.dart
/// 진폭이 높고 기타 주파수 범위에 있는 피크들을 기본음 후보로 선정
List<FftPeak> _identifyFundamentalCandidates(List<FftPeak> peaks) {
if (peaks.isEmpty) return [];
// 진폭 기준 내림차순 정렬
final sortedPeaks = List<FftPeak>.from(peaks);
sortedPeaks.sort((a, b) => b.magnitude.compareTo(a.magnitude));
// 상위 진폭 피크들을 기본음 후보로 선정
final double topMagnitude = sortedPeaks.first.magnitude;
final double threshold = topMagnitude * 0.6; // 최대 진폭의 60% 이상
final candidates = sortedPeaks
.where((peak) => peak.magnitude >= threshold)
.take(5) // 최대 5개까지
.toList();
return candidates;
}
기본음 후보 식별은 간단한 과정입니다.
기타 유효 대역 내에서, 진폭을 내림차순으로 정렬한 후, 최대 진폭의 60% 이상인 피크들을 최대 5개까지 기본음 후보로 간주합니다.
기본음이란, 배음의 원리를 설명드릴 때 말씀드렸던 배음의 원음으로, 감지된 연주 단위가 단일 타현인지, 다중현 타음인지 구분할 때 가장 중요하게 사용되는 데이터입니다.
절대값 대신 상대 임계를 사용하여 녹음 레벨(입력 볼륨)의 영향을 받지 않습니다.
이 단계에서 후볼르 좁혀 두면, 이후 배음 구조 평가 시 상위 피크의 분석 정확도가 올라가고, 잡음성 피크를 걸러내기에 용이합니다.
상위 피크 기반 점수
//fft_noise_filter.dart
/// 주요 피크 기반 분석 (NEW)
///
/// 진폭이 높은 상위 N개 피크만 추출하여 기타 연주와의 유사도를 평가
/// FFT 스펙트럼이 희소한 경우에도 주요 정보만으로 평가 가능
Map<String, dynamic> _analyzeTopPeaks(
List<FftPeak> allPeaks, List<FftPeak> fundamentalCandidates, double? currentPitch) {
// 충분한 피크가 없으면 낮은 점수 반환
if (allPeaks.isEmpty) {
return {'score': 0.0, 'topPeaks': <FftPeak>[]};
}
// 1. 상위 피크 선정 (진폭 기준 정렬)
final sortedPeaks = List<FftPeak>.from(allPeaks);
sortedPeaks.sort((a, b) => b.magnitude.compareTo(a.magnitude));
// 상위 6~8개 피크 또는 일정 threshold 이상 피크 선택
final int maxTopPeaks = 8; // 최대 사용할 상위 피크 수
final double magnitudeThreshold = sortedPeaks.first.magnitude * 0.2; // 최대 피크의 20% 이상 피크만 고려
final List<FftPeak> topPeaks =
sortedPeaks.where((peak) => peak.magnitude >= magnitudeThreshold).take(maxTopPeaks).toList();
// 2. 주요 피크 간 점수 계산
double score = 0.0;
// 2-1. 충분한 피크가 있는지 확인 (최소 2개)
if (topPeaks.length < 2) {
return {'score': 0.2, 'topPeaks': topPeaks}; // 매우 낮은 기본 점수 부여
}
// 2-2. 기본음 후보가 topPeaks에 포함되어 있는지 확인
int fundamentalInTopPeaks = fundamentalCandidates
.where((fund) => topPeaks.any((peak) => (peak.frequency - fund.frequency).abs() < 5.0))
.length;
double fundamentalBonus = math.min(0.3, fundamentalInTopPeaks * 0.15);
// 2-3. 기타 연주에 특화된 주요 피크 관계 분석
// 배음 관계 점검 (주요 피크들 간에 정수비 관계가 있는지)
int harmonicRelationships = 0;
for (int i = 0; i < topPeaks.length; i++) {
for (int j = i + 1; j < topPeaks.length; j++) {
final ratio = topPeaks[i].frequency / topPeaks[j].frequency;
final inverseRatio = topPeaks[j].frequency / topPeaks[i].frequency;
// 정수비에 가까운지 확인 (기타 배음 특성)
if (_isNearIntegerRatio(ratio) || _isNearIntegerRatio(inverseRatio)) {
harmonicRelationships++;
}
}
}
// 피크 수 대비 배음 관계 비율 계산
double maxPossibleRelationships = (topPeaks.length * (topPeaks.length - 1)) / 2;
double harmonicRatio = harmonicRelationships / math.max(1.0, maxPossibleRelationships);
// 2-4. 주파수 범위 검증 (기타 주파수 범위에 맞는지)
double minFreq = double.infinity;
double maxFreq = 0.0;
for (final peak in topPeaks) {
if (peak.frequency < minFreq) minFreq = peak.frequency;
if (peak.frequency > maxFreq) maxFreq = peak.frequency;
}
// 일반적인 기타 주파수 범위 체크 (80Hz ~ 1.3kHz)
bool isInGuitarRange = minFreq >= 80.0 && maxFreq <= 1320.0;
double rangeScore = isInGuitarRange ? 0.2 : 0.1;
// 2-5. 현재 피치와의 관계 점검 (제공된 경우)
double pitchMatchScore = 0.0;
if (currentPitch != null && currentPitch > 0) {
// topPeaks 중 현재 피치와 가까운 피크가 있는지 확인
bool hasPitchMatch = topPeaks.any((peak) =>
(peak.frequency / currentPitch - 1.0).abs() < 0.05 || // 직접 일치
(peak.frequency / (currentPitch * 2) - 1.0).abs() < 0.05 || // 옥타브 위
(peak.frequency / (currentPitch / 2) - 1.0).abs() < 0.05 // 옥타브 아래
);
pitchMatchScore = hasPitchMatch ? 0.2 : 0.0;
}
// 2-6. 최종 점수 계산
score = 0.3 + // 기본 점수
(fundamentalBonus) + // 기본음 보너스
(harmonicRatio * 0.3) + // 배음 관계 점수
rangeScore + // 주파수 범위 점수
pitchMatchScore; // 피치 일치 점수
// 0.0-1.0 범위로 제한
score = score.clamp(0.0, 1.0);
return {
'score': score,
'topPeaks': topPeaks,
'harmonicRelationships': harmonicRelationships,
'fundamentalInTopPeaks': fundamentalInTopPeaks,
};
}
진폭 상위 피크(최대 8개, 상위 피크의 20% 이상)를 골라 기타적 특성을 종합 점수로 환산합니다.
가산 요소는, ① 기본음 후보가 상위 피크에 포함돼 있는지(기본음 보너스), ② 피크 간 빈도 비율이 정수배/분수배에 근접한지(배음 관계), ③ 피크들이 일반적인 기타 범위(약 80–1320 Hz)에 분포하는지(범위 점수), ④ 외부로 전달된 currentPitch와 직접/옥타브 일치하는 피크가 있는지(피치 일치)입니다.
이 조합은 스펙트럼이 희소하거나 약간 왜곡돼도 기타 특유의 구조를 포착할 수 있도록 설계됐습니다.
상위 피크 기반 점수 - 정수비 근사치 검증 함수(보조)
//fft_noise_filter.dart
/// 정수비에 가까운지 확인하는 보조 함수
bool _isNearIntegerRatio(double ratio) {
if (ratio <= 1.1 || ratio > 10.0) return false; // 너무 작거나 큰 비율은 제외
final nearestInteger = ratio.round();
final difference = (ratio - nearestInteger).abs();
// 허용 오차 내에 있는지 확인 (값이 클수록 더 큰 오차 허용)
return difference <= (0.08 * nearestInteger);
}
두 피크의 주파수 비가 정수에 가까운지를 확인해 배음 관계를 판별합니다.
1.1 이하(거의 동일)나 10 초과(너무 벌어진 비율)는 제외하고, 정수 값이 클수록 허용 오차(±8%×정수)를 조금 넓혀 고차 배음의 변동성을 수용합니다. 이 판단이 많을수록 “기타다운” 배음 사다리가 존재한다고 볼 수 있습니다
배음 구조 평가
//fft_noise_filter.dart
/// 배음 구조 평가
///
/// 피크들 간의 배음 관계를 평가하여 배음 구조 점수를 계산합니다.
/// [peaks] 분석된 주파수 피크 목록
/// [fundamentalCandidates] 기본음 후보 목록
Map<String, dynamic> _evaluateHarmonicStructure(List<FftPeak> peaks, List<FftPeak> fundamentalCandidates) {
// 배음 관계가 명확한 피크 수 카운트
int harmonicCount = 0;
double harmonicScore = 0.0;
// 기본음 후보가 없으면 0점 반환
if (fundamentalCandidates.isEmpty) {
return {
'harmonicScore': 0.0,
'harmonicCount': 0,
};
}
// 가장 유력한 기본음 찾기
final bestFundamental = fundamentalCandidates.reduce(
(a, b) => a.magnitude > b.magnitude ? a : b,
);
// 배음 관계 분석 (V3-plus 호환 버전)
final fundamentalFreq = bestFundamental.frequency;
final harmonicPeaks = <FftPeak>[];
// 2-8배음 범위에서 배음 관계 확인
for (int harmonic = 2; harmonic <= 8; harmonic++) {
final expectedFreq = fundamentalFreq * harmonic;
// 8% 오차 허용으로 해당 배음과 일치하는 피크 찾기
final matchingPeak = peaks.firstWhere(
(peak) => (peak.frequency - expectedFreq).abs() / expectedFreq < 0.08,
orElse: () => FftPeak(frequency: 0, magnitude: 0, binIndex: 0),
);
if (matchingPeak.frequency > 0) {
harmonicPeaks.add(matchingPeak);
harmonicCount++;
}
}
harmonicCount += 1; // 기본음 자체 포함
// 배음 구조 점수 계산
if (harmonicCount >= 1) {
// 1. 기본 배음 개수 점수 (최대 0.7)
final countScore = math.min(0.7, harmonicCount / 5.0);
// 2. 기본음의 강도 점수 (최대 0.3)
final fundamentalStrengthScore = bestFundamental.magnitude * 0.3;
// 3. 배음 강도의 분포 평가 - 이상적인 배음은 고차 배음일수록 진폭이 감소
double distributionScore = 0.0;
if (harmonicPeaks.isNotEmpty) {
// 배음들이 적절히 감소하는 패턴인지 확인
double totalHarmonicMagnitude = harmonicPeaks.fold(0.0, (sum, peak) => sum + peak.magnitude);
double averageHarmonicMagnitude = totalHarmonicMagnitude / harmonicPeaks.length;
// 기본음 대비 배음들의 평균 크기가 적절한지 평가
if (averageHarmonicMagnitude < bestFundamental.magnitude) {
distributionScore = 0.2; // 정상적인 감소 패턴
} else {
distributionScore = 0.1; // 비정상적인 패턴
}
}
// 종합 배음 점수
harmonicScore = countScore + fundamentalStrengthScore + distributionScore;
// 0.0-1.0 범위로 제한
harmonicScore = harmonicScore.clamp(0.0, 1.0);
}
return {
'harmonicScore': harmonicScore,
'harmonicCount': harmonicCount,
'fundamentalFreq': fundamentalFreq,
'harmonicPeaks': harmonicPeaks.length,
};
}
가장 유력한 기본음을 기준으로 2–8배 배음 위치에 해당하는 피크를 8% 오차 내에서 탐색해 개수를 셉니다.
점수는 ① 배음 개수(최대 0.7), ② 기본음의 강도(최대 0.3), ③ 배음 진폭이 기본음 대비 자연스럽게 감쇠하는지(분포 점수)로 구성됩니다.
결과에는 harmonicCount, fundamentalFreq 등 메타데이터도 함께 담겨 상위 로직(가중 결합·로깅)에 활용됩니다.
에너지 분포 기반 분석 (저-중-고 비율)
//fft_noise_filter.dart
/// 주파수 에너지 분포 분석
///
/// FFT 데이터의 주파수 에너지 분포를 분석하여 점수화합니다.
/// [fftData] FFT 진폭 데이터
///
/// 반환값: 기타 특성과 일치하는 정도 (0.0 ~ 1.0)
double _analyzeFrequencyDistribution(List<double> fftData) {
if (fftData.isEmpty) return 0.0;
// 샘플링 레이트와 FFT 크기 기본값 (FftAnalyzer와 동일 값 사용)
final double sampleRate = 44100.0;
final int fftSize = 4096;
// 유효 FFT 범위 계산
final halfFftSize = fftSize ~/ 2;
final effectiveLength = math.min(fftData.length, halfFftSize);
// 주파수 범위 구분 (저역, 중역, 고역)
final lowFreqLimit = (_minGuitarFreq * fftSize / sampleRate).floor();
final midFreqLimit = (500.0 * fftSize / sampleRate).floor();
final highFreqLimit = (_maxGuitarFreq * fftSize / sampleRate).floor();
// 각 범위의 에너지 합계
double lowFreqEnergy = 0.0;
double midFreqEnergy = 0.0;
double highFreqEnergy = 0.0;
double totalEnergy = 0.0;
// 각 범위별 에너지 계산
for (int i = 0; i < effectiveLength; i++) {
final energy = fftData[i];
totalEnergy += energy;
if (i < lowFreqLimit) {
// 저역은 무시 (DC 성분 및 매우 낮은 주파수)
} else if (i < midFreqLimit) {
lowFreqEnergy += energy;
} else if (i < highFreqLimit) {
midFreqEnergy += energy;
} else {
highFreqEnergy += energy;
}
}
// 에너지가 없으면 0점
if (totalEnergy <= 0.00001) {
// 기존 0.0001에서 더 낮춤
return 0.0;
}
// 각 대역의 에너지 비율
final lowFreqRatio = lowFreqEnergy / totalEnergy;
final midFreqRatio = midFreqEnergy / totalEnergy;
final highFreqRatio = highFreqEnergy / totalEnergy;
// 이상적인 기타 스펙트럼 분포와 비교 (경험적 값)
// 기타는 일반적으로 저-중역에 에너지가 집중됨
// 분포 점수 계산 - 저역 35%, 중역 45%, 고역 20% 정도가 이상적
double distributionScore = 0.0;
// 저역 점수 (약 30-40% 정도가 이상적)
double lowScore = 1.0 - math.min(1.0, (lowFreqRatio - 0.35).abs() / 0.25); // 허용 오차 범위 확대
// 중역 점수 (약 40-50% 정도가 이상적)
double midScore = 1.0 - math.min(1.0, (midFreqRatio - 0.45).abs() / 0.25); // 허용 오차 범위 확대
// 고역 점수 (약 10-20% 정도가 이상적)
double highScore = 1.0 - math.min(1.0, (highFreqRatio - 0.15).abs() / 0.15); // 허용 오차 범위 확대
// 가중 평균 (중역과 저역을 더 중요하게 고려)
distributionScore = (lowScore * 0.35) + (midScore * 0.45) + (highScore * 0.2);
return distributionScore;
}
샘플링레이트/FFT 크기(44.1kHz/4096)를 가정해 저·중·고역 대역을 구분하고, 각 대역 에너지 비율을 계산합니다.
기타의 경험적 분포(저 35%, 중 45%, 고 15% 내외)에 가까울수록 높은 점수를 부여하며, 허용 오차를 다소 넓혀 현실 신호(마이킹·환경·이펙팅)에 견고하게 대응합니다.
피크가 희소하거나 폴리/리듬성 노이즈로 스펙트럼이 넓게 번진 경우에도 유효한 대체 판단 근거로 작동합니다.
시간적 일관성 검증(과거 결과와 비교)
//fft_noise_filter.dart
/// 시간적 일관성 필터링 적용
///
/// 과거 결과와 현재 결과를 가중 평균하여 시간적으로 일관된 결과를 생성합니다.
double _applyTemporalSmoothing(double currentConfidence) {
// 이력이 없으면 현재 값 그대로 반환
if (_resultHistory.isEmpty) {
return currentConfidence;
}
// 이전 결과들의 평균 신뢰도 계산
double historyAverage =
_resultHistory.map((result) => result.confidence).reduce((a, b) => a + b) / _resultHistory.length;
// 가중 평균 계산
return (_temporalSmoothingFactor * historyAverage) + ((1.0 - _temporalSmoothingFactor) * currentConfidence);
}
최근 결과 이력(최대 3개)의 평균과 현재 값을 temporalSmoothingFactor=0.7로 지수가중평균해 순간적 스파이크나 단발성 미스를 완화합니다.
이로써 실시간 판정의 깜빡임을 줄이고, UI/후속 모듈에서 안정적인 신뢰도 흐름을 확보합니다. 이력은 매 프레임 누적·유지됩니다.
//fft_noise_filter.dart
// 10. 결과 생성
final result = FftSoundClassificationResult(
confidence: smoothedConfidence,
isGuitarSound: smoothedConfidence >= _guitarConfidenceThreshold,
timestamp: now,
metadata: metadata,
);
return result;
이로써 위의 로직들을 거쳐, 최종적으로 환산된 점수들을 종합적으로 평가한 값인 smoothedConfidence를 기반으로 기타 연주 판정을 내립니다.
한계
이렇듯, 굉장히 정교하고 짜임새있는 로직처럼 보이지만, 사실 이 로직에도 허점이 몇 가지 있습니다.
다음은 제가 이 로직을 기반으로 실제 테스트를 거치며 겪었던 문제 상황들과, 최종적으로 YAMNet 모델을 통한 머신러닝 기반 분류기로 업그레이드 하게 된 이유들을 나열합니다.
비기타 소리를 기타 소리로 인식하는 케이스가 잦음
제 로직의 핵심 판단 기준은 오디오 데이터의 배음 구조 입니다. 기타와 비슷하거나 로직에서 유의미하다고 판별할수 있는 정수배 배음 구조를 지닌 소리가 입력되면, 기타가 아님에도 분류기의 기준을 통과하는 사례가 없지 않았습니다.
보컬, 신디사이저, 피아노 등의 경우가 이러합니다. 이들은 기타와 마찬가지로 정수배 배음 구조를 가집니다. 특히 보컬은 기음과 배음의 조합으로 특정 음색을 만드는데, 이는 기타와 유사한 패턴을 띄어 룰 베이스 로직이 오판할 확률이 높습니다.
기타 사운드 내에서도 특정 케이스에서 분류 실패가 잦음
기타 사운드 내에서도, 특정 주법이나 소리 특성에서 해당 사운드를 기타 사운드로 감지하지 못하는 경우가 잦았습니다.
예시로, 펑크 장르에서 자주 활용되는 팜 뮤트나 퍼커시브 사운드의 경우, 필연적으로 마이크에 피크로 쇠줄을 타현하는 소리가 같이 잡히게 됩니다. 이는 배음 구조가 없는 물리적 타격음이라, 기타 사운드로 분류하기 어려운 케이스가 됩니다.
이 외에도, 극단적인 저음역대 연주(6번줄 0~3번 프랫 등)나, 반대의 사례인 극단적인 고음역대 연주(16프랫 이상)의 경우, 에너지 분포가 특정 음역대에 너무 몰려, 규칙적인 배음 구조가 보이지 않게 되어 분류에 실패하는 경우가 있습니다.
다양한 환경에 대한 대응 불가
이 문제는 바로 위 문제와 이어집니다.
기타리스트에게 다양한 환경 이라고 하면, 실제로 연주를 진행하는 물리적 환경도 포함되지만, 소리 특성 자체도 포함됩니다.
기타라는 악기는 종류에 따른 소리의 특성도 다양하고, 특히 일렉트릭 기타의 경우 이펙터나 앰프를 조작하여 전자적으로 셀 수 없이 많은 스타일의 소리를 만들어낼 수 있습니다.
즉, 우리의 분류기 로직은 클래식 기타로 만들어내는 보사노바 연주부터, 강력한 오버드라이브와 디스토션이 맞물린 헤비메탈 톤까지 모두 커버할 수 있어야 합니다.
이펙터는 원음의 배음 구조를 인위적으로 왜곡하고 새로운 주파수 성분(잡음)을 생성하기 때문에, 배음의 자연스러운 감쇠 패턴을 분석하는 룰 베이스 로직은 이러한 변화를 기타 사운드로 인식하기 어렵습니다.
특히 디스토션/오버드라이브 등의 이펙터로 고역 잡음이 과다해지면 배음이 깔끔하게 감쇠하는 이상형이 깨져 오판정이 나올 수 있습니다.
그렇다고 일렉트릭 기타 사용자만을 대상으로 잡아버리면, 분류기의 통과 기준이 너무 느슨해져 일반적인 소음도 기타 사운드로 분류되는 문제가 나타나버립니다.
단일 프레임 기반 분류의 한계
지금의 로직은 프레임 단위 의사결정이라 상위 맥락(연속 연주 흐름)을 충분히 보지 못합니다.
로직의 추후 목적이 단순히 기타/비기타 사운드 분류를 넘어 연주 내의 맥락을 파악하는 것이긴 했지만, 이를 차치하고서도 프레임 기반 분류는 정확도가 낮습니다.
예시로, 도중에 한 프레임이 갑작스러운 소음의 영향을 받아 피치가 기타 가역대를 벗어나는 경우, 분류기는 이를 기타 사운드로 분류하지 못합니다.
로직의 최종 판별 과정에 시간적 연속성 기반 점수 체계를 넣었으나, 이 또한 완벽하진 않았습니다.
이대로는 안된다
이렇듯, 문제가 한두개가 아닙니다.
제가 포스트 초반에 삽질이라는 표현을 쓴 것이 괜히 그랬던게 아닙니다.
지금까지의 문제를 종합해보면, 우리의 로직이 목표에 도달하려면,
- 배음 구조 외의 기타만의 사운드 특성을 파악할수 있어야 하며,
- 이펙터나 녹음 환경 등에 구애받지 않을 정도로 범용적인 판단 기준이 있어야 하고,
- 시간적 연속성을 고려한 판단 기준이 있어야 합니다.
물론 이러한 요구사항을 수집하고, 기타 사운드를 분류하는 방식을 학습한 것만으로도 지금까지의 과정이 마냥 무의미한 삽질이 아닐 것입니다.
그렇다고 문제가 해결된 건 아닙니다. 위 요구사항을 만족시키기 위한 다른 방식의 접근이 필요했고, 해결법을 찾던 와중에 YAMNet 모델이 제 눈에 들어왔습니다.
YAMNet은 구글에서 공개한 오픈소스 모델로, 오디오 소스를 입력받아 사전에 학습된 소리 클래스 중 가장 유사한 클래스를 추론하는 모델입니다.
구글에서 이미 유튜브 음원 크롤링을 통해 방대한 양의 기타 사운드(및 음악 관련 사운드)를 학습시켜 분류 대상으로 설정해두었기에, 상기에 언급한 요구사항을 상당수 만족할수 있을 것으로 보입니다.
마치며, 그리고…
이번 포스트는, 최종적으로 머신러닝 기반 분류기로 업그레이드 하게 된 이유와 그 과정을 설명하는 것이 목적이었습니다.
블로그의 가벼운 문체를 유지하기 위해 삽질 이라는 표현을 썼지만, 사실 완전한 삽질은 아닙니다.
룰 베이스 로직을 개발하면서 FFT 스펙트럼의 형태와, 방대한 종류의 기타 사운드의 여러 특성에 대해 조금 더 이해할수 있게 되었습니다.
오늘 보여드린 룰 베이스 기타 사운드 분류기는 사실상 폐기되겠지만, 내부 소스코드를 재활용하여 앱 내 다른 기능에 활용하도록 리팩토링 중입니다.
더불어, 룰 베이스 로직의 한계를 인식하고 머신러닝 기반의 분류기로 업그레이드해야할 필요성을 느끼게 되었습니다.
이 점은 다음 포스트에서 더 자세하게 다루도록 하겠습니다.
모자라고 긴 글 읽어주셔서 감사합니다.
다음 포스트에서 뵙겠습니다!